ΓΥΜΝΑΣΙΟ
ΦΙΛΙΑΤΡΩΝ ΤΑΞΗ Γ1
ΥΠΕΥΘΥΝΟΣ: ΓΙΑΝΝΑΚΟΠΟΥΛΟΣ
ΣΤΑΜΑΤΗΣ
ΚΑΘΗΓΗΤΗΣ
ΜΑΘΗΜΑΤΙΚΩΝ
ΕΡΓΑΣΙΑ ΣΤΑ
ΜΑΘΗΜΑΤΙΚΑ
ΕΠΩΝΥΜΟ: ΓΙΑΝΝΑΚΟΠΟΥΛΟΥ
ΟΝΟΜΑ : ΜΑΤΙΝΑ
ΗΜΕΡΟΜΗΝΙΑ: 31
Μαρτίου 2001
ΤΙΤΛΟΣ
ΕΡΓΑΣΙΑΣ
Υπολογισμός του ύψους
ενός
ψηλού
αντικειμένου.
Θέλουμε
να
μετρήσουμε το ύψος
του
Πύργου
του
Άϊφελ
(ομοίωμα στα
Φιλιατρά ) με χρήση
του
κεφαλαίου 7
της Τριγωνομετρίας.
Να
περιγραφεί ο
τρόπος
μέτρησης καθώς και τα
όργανα
που
θα χρησιμοποιηθούν. Ύστερα να γίνει
ο υπολογισμός του ύψους
του.
ÄÄÄÄÄÄÄÄÄÄÄÄÄÄÄÄÄÄÄÄÄÄÄÄÄÄÄÄÄÄÄÄÄÄÄÄÄÄÄÄÄÄÄÄ
|
|
Ομοίωμα του πύργου του Άϊφελ
βρίσκεται στα Φιλιατρά
Μεσσηνίας στην είσοδο της πόλης από το μέρος
της
Κυπαρισσίας. Δεν
περνάνε βέβαια τα
αυτοκίνητα κάτω από τον πύργο, αλλά δίπλα. Ο
πύργος
είναι
δωρεά
του Χαράλαμπου
Φουρναράκη και
στήθηκε σε
αυτή
τη
θέση
υπό
την
επίβλεψή του. Πολλοί
τουρίστες
σταματούν και
φωτογραφίζουν τον πύργο, ο
οποίος
πολλά
βράδια
είναι
φωταγωγημένος. Λόγω του
μεγάλου ύψους
του
έχει
και
αλεξικέραυνο. Δίπλα του είναι
το
Πρώτο
Δημοτικό
Σχολείο Φιλιατρών. |
|
Περιγραφή του τρόπου μέτρησης. Την
Πέμπτη
22-3-2001
στις 16:00 πήγαμε όσοι μαθητές και
μαθήτριες θέλαμε στον χώρο του πύργου όπου μας
περίμενε ο
καθηγητής μας των
Μαθηματικών κ.
Γιαννακόπουλος
Σταμάτης, ο
οποίος
είχε
φέρει
μαζί
του
μία
μετροταινία και ένα
«ταχύμετρο». Αφού κάναμε
«αναγνώριση του χώρου»
διαλέξαμε ένα σημείο μέσα στο προαύλιο του πρώτου Δημοτικού
Σχολείου, από το οποίο
είχαμε
ορατή
και
την
βάση
του
πύργου
και
την
κορυφή
του. Στήσαμε τον
τρίποδα του
ταχυμέτρου
και
στερεώσαμε το όργανο στη
βάση
του
πάνω
στον
τρίποδα.
Ύστερα
οριζοντιώσαμε το ταχύμετρο
με τους
κοχλίες. Επεξεργαστήκαμε για λίγη ώρα το ταχύμετρο να δούμε
πώς
λειτουργεί. Παρατηρήσαμε ότι τις γωνίες τις
μετράει σε βαθμούς και όχι σε μοίρες. Σκοπεύσαμε με την
διόπτρα του
την
κορυφή
του
πύργου
(το
πιο
ψηλό
του
σημείο)
και διαβάσαμε την
ένδειξη του
οργάνου: 75,61
βαθμοί.
Κατόπιν
σκοπεύσαμε με την
διόπτρα τη
βάση
του
πύργου
και
διαβάσαμε την
ένδειξη του
οργάνου: 100
βαθμοί. Με
την
μετροταινία μετρήσαμε επί του
εδάφους από
την
βάση
του
οργάνου
(κέντρο
του
τρίποδα)
μέχρι
την
βάση
του
πύργου και
βρήκαμε την
απόσταση αυτή ίση με 43,30
μέτρα.
Η
διόπτρα του
οργάνου ήταν
σε
ύψος 1,50 μέτρα από το έδαφος. Με
τα
στοιχεία αυτά
μπορούμε να
υπολογίσουμε το ύψος
του
πύργου. |
Περιγραφή των
οργάνων που
θα
χρησιμοποιηθούν: 1) Μία μετροταινία
50 μέτρων για
την
μέτρηση ενός
μήκους. 2) Ένα όργανο
μέτρησης κατακόρυφων γωνιών όπως είναι το «ταχύμετρο».
Το
ταχύμετρο το
δανείστηκε από την
Τεχνική
εταιρεία «DS» (που
κατασκευάζει αυτή την
περίοδο το γεφύρι και τον δρόμο
Κυπαρισσίας-Φιλιατρών)
ο καθη-γητής μας κ.
Γιαννακόπουλος
Σταμάτης με την
μεσολάβηση του κ.
Χαρ.
Λίτσα. Το
ταχύμετρο
μετράει οριζόντιες και
κατακόρυφες γωνίες σε βαθμούς. 400
βαθμοί
ισοδυ-ναμούν με 360
μοίρες. Τα είδωλα
μέσα
από
την
διόπτρα του
φαίνονται «αντεστραμμένα». Ο
πύργος
όπως
είναι
σήμερα: (από το βορινό μέρος)
|
|
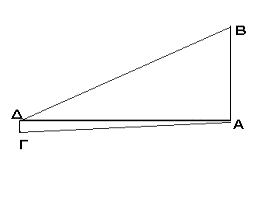
Υπολογισμός του ύψους: Ο
πύργος
παριστάνεται από την κάθετη πλευρά ΑΒ του
διπλανού σχήματος. Το ταχύμετρο είναι στην θέση ΓΔ. Η
διόπτρα του
είναι
στο
σημείο
Δ. Είναι ΓΔ = 1,50 μέτρα. Η
ΑΓ = 43,30
μέτρα.
Το
τρίγωνο ΑΔΓ
είναι
ορθογώνιο στην κορυφή του Δ
(είχαμε
μία
κλίση
του
εδάφους) και
με το
Πυθαγόρειο
Θεώρημα βρίσκουμε πρώτα την ΑΔ ίση
με 43,27 m. Το
τρίγωνο ΑΒΔ
είναι
ορθογώνιο με Α=900
και
γωνία
ΑΔΒ = ω = 220. Από
την
τριγωνομετρία (κεφάλαιο 7 )
γνωρίζουμε ότι:
Αλλά ΑΔ =
43,27
μέτρα, και
εφω = εφ220 = 0,404 Επομένως ΑΒ = 43,27 m . 0,404 ή ΑΒ = 17,48 m Συνεπώς το ζητούμενο ύψος του πύργου είναι ΑΒ =
17,48 μέτρα. Παρατήρηση: Επειδή η
ΑΓ
και η ΑΔ είναι
σχεδόν
ίσες
(διαφέρουν κατά 0,03 μέτρα) θα
μπορούσαμε να μην
πάρουμε καθόλου το τρίγωνο ΑΓΔ. Τότε η
ΑΒ θα προκύψει ίση με 43,30 . 0,404 ή ΑΒ = 17,49 μέτρα δηλαδή
ασήμαντη
διαφορά από
την
τιμή
που
υπολογίσαμε
προηγουμένως. |
Σχήμα
Μετατροπή της γωνίας από
βαθμούς σε
μοίρες: Η
γωνία
ΑΔΒ = ω
σε βαθμούς είναι: 100 - 75,61 = 24,39 και
επειδή
400
βαθμοί
ισοδυναμούν με 360
μοίρες,
οι 24,39 βαθμοί θα
ισοδυναμούν με ω = 360 . 24,39 / 400 ή ω = 22 μοίρες ω=220 |
|
|
Το
ταχύμετρο είναι ένα
γωνιομετρικό όργανο που
χρησιμεύει για την ταχεία
γραφική αποτύπωση του
εδάφους. Λέγεται και μικρός Θεοδόλιχος και
χρησιμοποιείται για την
μέτρηση
οριζόντιων ή
κατακόρυφων γωνιών και τη μέτρηση
αποστάσεων όλων των ορατών σημείων, με την
βοήθεια της
σταδίας
(αριθμημένου κανόνα). Η
διόπτρα του,
εκτός
από
το
σταυρόνημα, φέρει
διάταξη από
δύο
οριζόντια νήματα που επιτρέπουν τη μέτρηση των
αποστάσεων οπτικά. Γι αυτό
η
διόπτρα του
λέγεται
«σταδιομετρική
διόπτρα» Τα κύρια μέρη ενός ταχύμετρου είναι: 1) Η βάση με το
τρικόχλιο. 2) Ο
πρωτεύοντας άξονας με τον
οριζόντιο κύκλο για την ανάγνωση των
οριζόντιων γωνιών. 3) Ο
δευτερεύον άξονας στον οποίο
περιστρέφεται η
διόπτρα με
τον
κατακόρυφο κύκλο για την
ανάγνωση των
κατακόρυφων γωνιών. 4) Κάλυμμα του
οριζόντιου κύκλου με δίκρανα και τα συστήματα
ανάγνωσης
(οριζόντιων και
κατακόρυφων )
γωνιών. 5) Αεροστάθμες. |